【Member Papers】Feasibility of p-type conduction in beta rhodium alloyed gallium oxide
日期:2025-09-25阅读:230
Researchers from the Shenzhen Pinghu Laboratory have published a dissertation titled "Feasibility of p-type conduction in beta rhodium alloyed gallium oxide" in Journal of Applied Physics.
Project Support
The authors acknowledge financial support from the Shenzhen Pinghu Laboratory Project (Grant No. 224110) and the computing resources from the National Supercomputing Center in Shenzhen.
Background
Metal oxides have extensive applications in various fields, including dielectrics, supercapacitor electrodes, photocatalysts, thin-film transistors, and others. However, most oxides' valence band maxima (VBMs) mainly consist of deep and localized oxygen 2p orbitals, leading to low hole mobility and the presence of deep acceptors. In 1997, Kawazoe et al. proposed a chemical design concept for p-type metal oxides. According to this concept, to mitigate the localization of the valence band edge, cationic species should possess orbitals, such as nd10, whose energy is almost comparable to that of oxygen 2p orbitals. This allows the formation of covalent bonds with oxide ions. Additionally, crystal lattice fields, such as tetrahedral or octahedral coordination of oxide ions, can strengthen these covalent bonds and further reduce the localization of the oxygen 2p orbital. Based on this concept, several p-type metal oxides have been developed, such as Cu2O, SnO, and spinel ZnRh2O4. Despite these advancements, employing these p-type materials in power electronics remains a formidable challenge. Cu2O often co-mixes with Cu and CuO. SnO easily converts into SnO2 via oxidation and thus exhibits n-type behavior. ZnRh2O4 has a relatively small bandgap, approximately 2.1 eV. NiO, a commonly used p-type oxide, still suffers from insufficient hole mobility. In essence, oxides with both ultrawide bandgaps and favorable p-type conduction characteristics are yet to be discovered and explored.
Abstract
Beta-gallium oxide (β-Ga2O3) has attracted extensive attention in the field of power devices owing to its ultrawide bandgap and well-established synthesis method. However, the lack of p-type conductivity in β-Ga2O3 limits the device performance. Recently, rhodium-alloyed β-Ga2O3, namely, β-(RhxGa1−x)2O3, has been predicted to possess elevated valence band maxima (VBMs) and reduced hole masses. This study explores the feasibility of realizing p-type doping in β-(RhxGa1−x)2O3. The acceptor levels for Li, Na, and Cu dopants in β-(Rh0.25Ga0.75)2O3 are determined to be lower than 0.4 eV from the VBMs. The elevation of the VBM, along with a weak interaction between the dopants' orbitals and the orbitals at the VBMs, plays a crucial role in facilitating the attainment of a shallow acceptor level. At a hole density of 1017 cm−3 and room temperature, the hole mobility of β-(Rh0.5Ga0.5)2O3 is predicted to reach 10.7 cm2 V−1 s−1, which is higher than the values of most p-type metal oxides. Moreover, the hole mobility is determined to be anisotropic, and its magnitude is mainly limited by polar optical phonon scattering. Our work shows that achieving p-type doping in β-(RhxGa1 − x)2O3 alloys is indeed feasible, and the formation of p–n homojunctions based on β-(RhxGa1 − x)2O3 could significantly extend the application scope of alloy oxides.
Conclusion
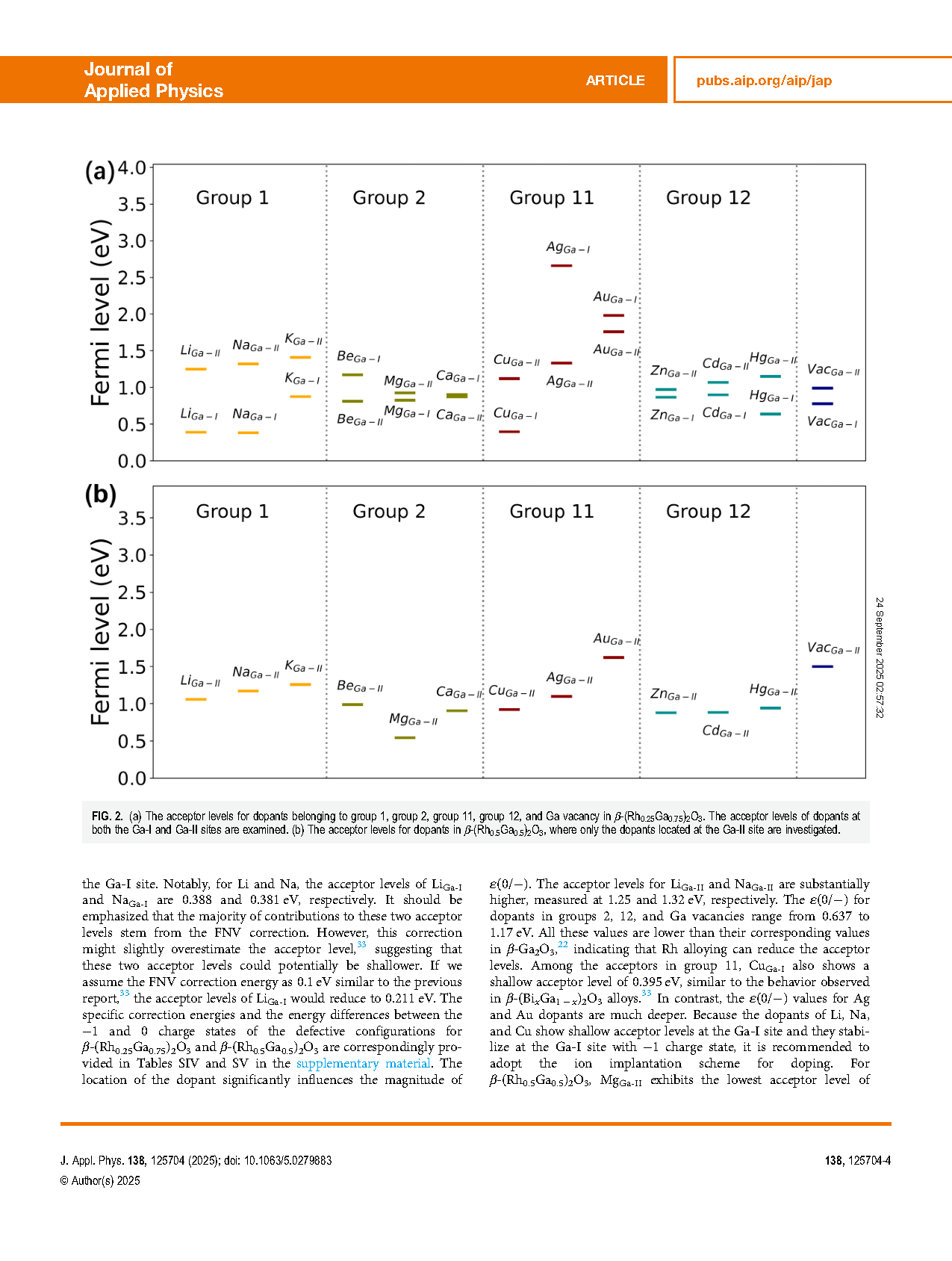
In summary, our research has delved into the feasibility of p-type conduction within the β-(RhxGa1 − x)2O3 alloys. We investigated possible p-type doping strategies for β-(Rh0.25Ga0.75)2O3 and β-(Rh0.5Ga0.5)2O3, along with the hole mobilities of β-(RhxGa1 − x)2O3 over the range of 0 ≤ x ≤ 0.5. Regarding the p-type doping schemes, we considered dopants such as Li, Na, K, Be, Mg, Ca, Cu, Ag, Au, Zn, Cd, Hg, and Ga vacancies. The valence band energies and the bonding behaviors of these dopants play crucial roles in determining the magnitude of acceptor levels. For a specific dopant in a similar location, the acceptor level decreases as the valence energy increases. In β-(Rh0.5Ga0.5)2O3, the acceptor level of the Mg dopant was determined to be 0.543 eV. The acceptor levels of Li and Na dopants at the octahedral Ga site are significantly lower than those at the tetrahedral Ga site, with values of 0.388 and 0.381 eV, respectively. These lower acceptor levels can be ascribed to the weaker interactions between the dopants' orbitals and the orbitals at the valence band maxima. For the hole mobilities, the β-(RhxGa1 − x)2O3 alloys typically show higher values compared to β-Ga2O3. Notably, this is particularly true for β-(Rh0.25Ga0.75)2O3 and β-(Rh0.5Ga0.5)2O3. At room temperature, the hole mobility of β-(Rh0.5Ga0.5)2O3 reaches 10.7 cm2 V−1 s−1 at a hole concentration of 1017 cm−3, which is higher than the values of most p-type metal oxides. The hole mobility displays strong anisotropy, and its magnitude is limited by polar optical scattering. Overall, the β-(RhxGa1 − x)2O3 alloys generally possess much shallower acceptor levels and higher hole mobilities compared to β-Ga2O3. Our predicted properties suggest that it is indeed feasible to achieve p-type conduction in β-(RhxGa1 − x)2O3 alloys. Given their ultrawide bandgaps, these alloys hold potential applications in high-power devices, deep ultraviolet optoelectronics, CMOS technology, and other areas.
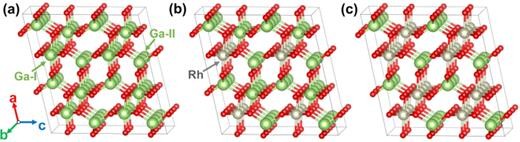
FIG. 1. (a)–(c) Illustrate the side views of β-Ga2O3, β-(Rh0.25Ga0.75)2O3, and β-(Rh0.5Ga0.5)2O3, respectively. The Ga, O, and Rh atoms are symbolized by green, red, and gray circles, correspondingly.

FIG. 2. (a) The acceptor levels for dopants belonging to group 1, group 2, group 11, group 12, and Ga vacancy in β-(Rh0.25Ga0.75)2O3. The acceptor levels of dopants at both the Ga-I and Ga-II sites are examined. (b) The acceptor levels for dopants in β-(Rh0.5Ga0.5)2O3, where only the dopants located at the Ga-II site are investigated.
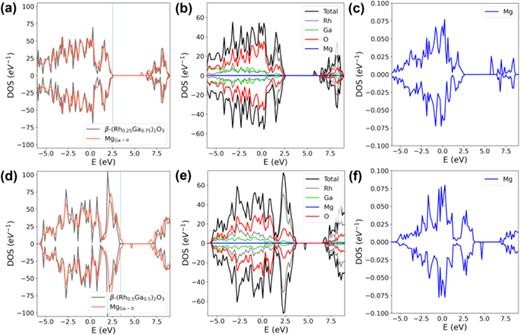
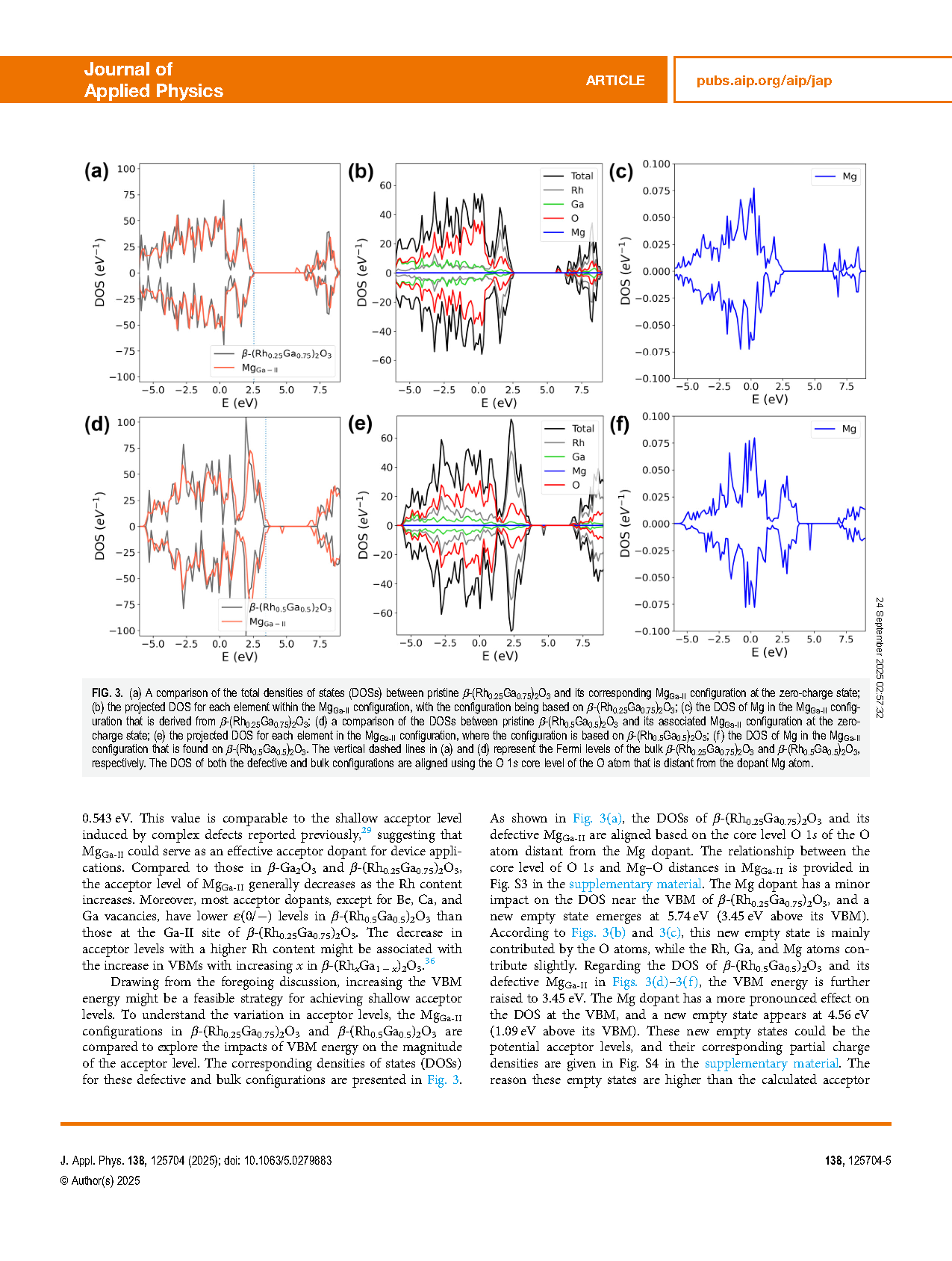
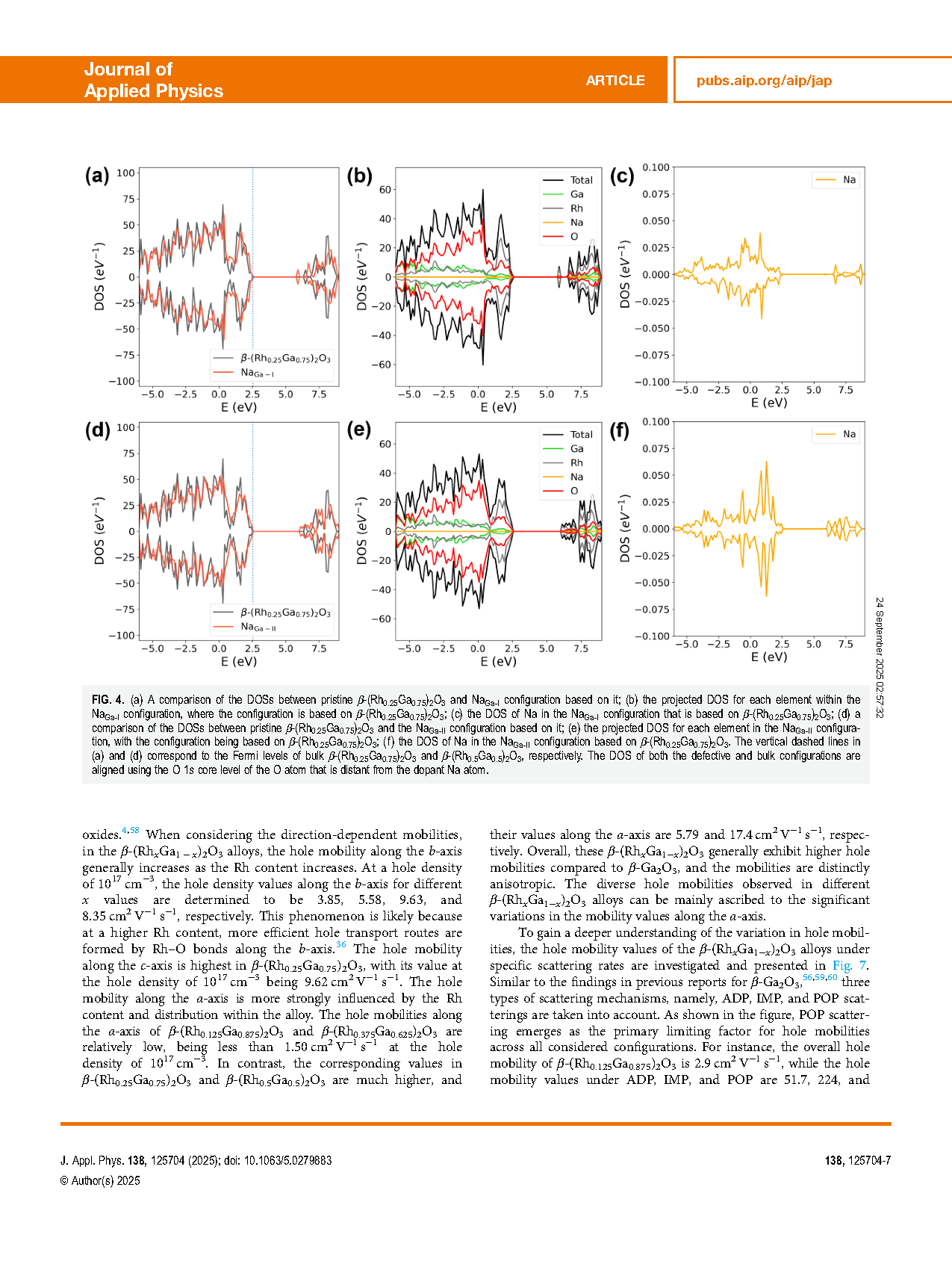
FIG. 3. (a) A comparison of the total densities of states (DOSs) between pristine β-(Rh0.25Ga0.75)2O3 and its corresponding MgGa-II configuration at the zero-charge state; (b) the projected DOS for each element within the MgGa-II configuration, with the configuration being based on β-(Rh0.25Ga0.75)2O3; (c) the DOS of Mg in the MgGa-II configuration that is derived from β-(Rh0.25Ga0.75)2O3; (d) a comparison of the DOSs between pristine β-(Rh0.5Ga0.5)2O3 and its associated MgGa-II configuration at the zero-charge state; (e) the projected DOS for each element in the MgGa-II configuration, where the configuration is based on β-(Rh0.5Ga0.5)2O3; (f) the DOS of Mg in the MgGa-II configuration that is found on β-(Rh0.5Ga0.5)2O3. The vertical dashed lines in (a) and (d) represent the Fermi levels of the bulk β-(Rh0.25Ga0.75)2O3 and β-(Rh0.5Ga0.5)2O3, respectively. The DOS of both the defective and bulk configurations are aligned using the O 1s core level of the O atom that is distant from the dopant Mg atom.
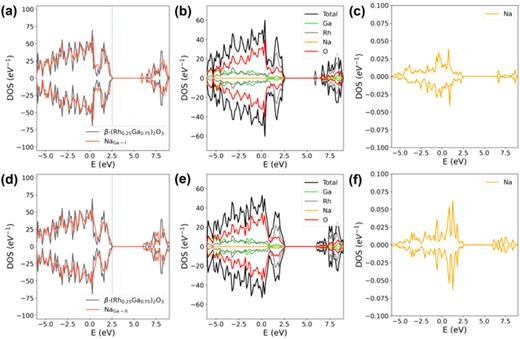
FIG. 3. (a) A comparison of the total densities of states (DOSs) between pristine β-(Rh0.25Ga0.75)2O3 and its corresponding MgGa-II configuration at the zero-charge state; (b) the projected DOS for each element within the MgGa-II configuration, with the configuration being based on β-(Rh0.25Ga0.75)2O3; (c) the DOS of Mg in the MgGa-II configuration that is derived from β-(Rh0.25Ga0.75)2O3; (d) a comparison of the DOSs between pristine β-(Rh0.5Ga0.5)2O3 and its associated MgGa-II configuration at the zero-charge state; (e) the projected DOS for each element in the MgGa-II configuration, where the configuration is based on β-(Rh0.5Ga0.5)2O3; (f) the DOS of Mg in the MgGa-II configuration that is found on β-(Rh0.5Ga0.5)2O3. The vertical dashed lines in (a) and (d) represent the Fermi levels of the bulk β-(Rh0.25Ga0.75)2O3 and β-(Rh0.5Ga0.5)2O3, respectively. The DOS of both the defective and bulk configurations are aligned using the O 1s core level of the O atom that is distant from the dopant Mg atom.
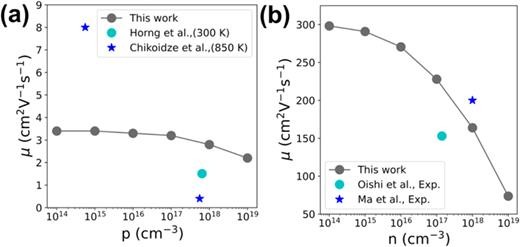
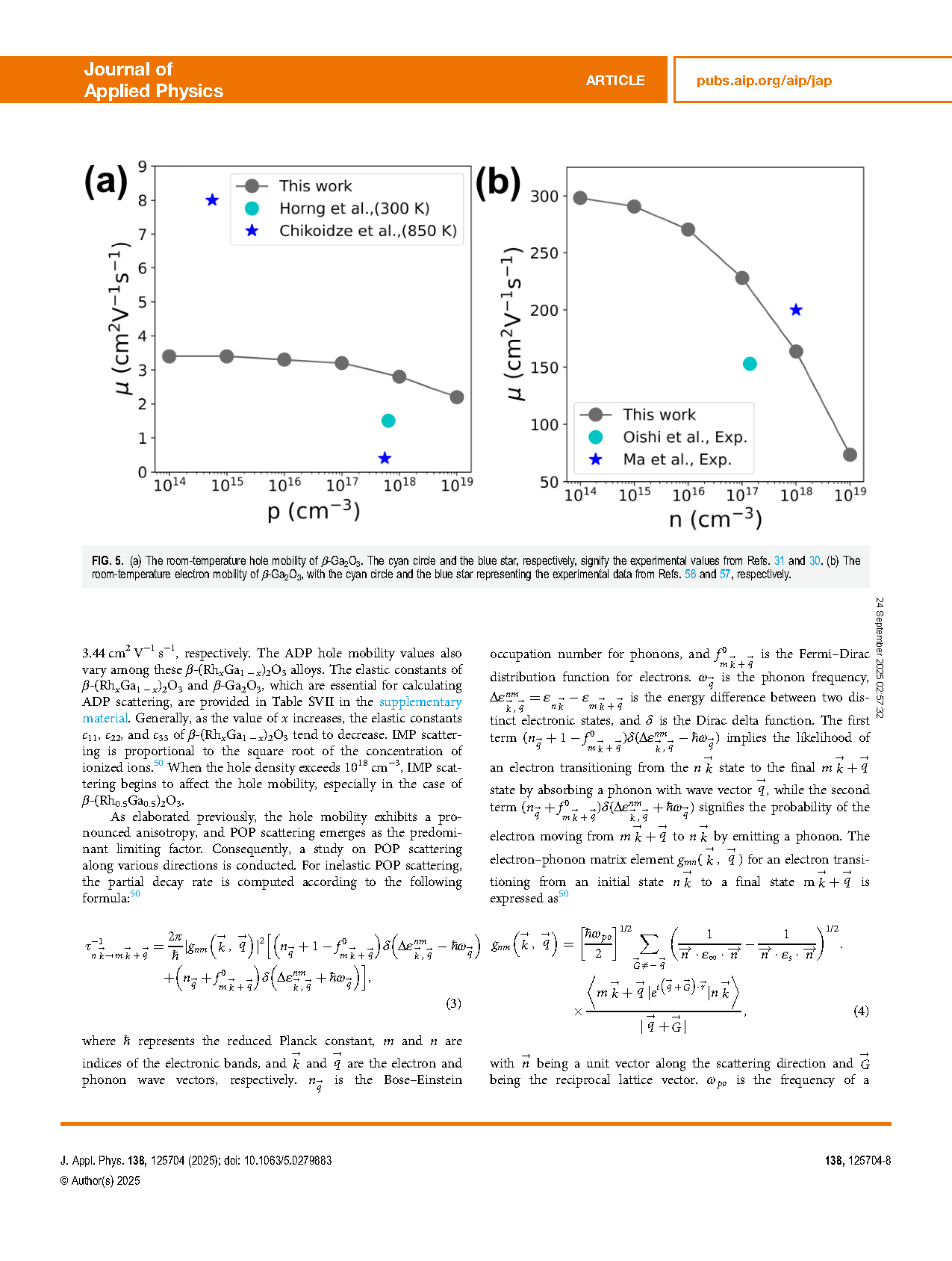
FIG. 5. (a) The room-temperature hole mobility of β-Ga2O3. The cyan circle and the blue star, respectively, signify the experimental values from Refs. 31 and 30. (b) The room-temperature electron mobility of β-Ga2O3, with the cyan circle and the blue star representing the experimental data from Refs. 56 and 57, respectively.
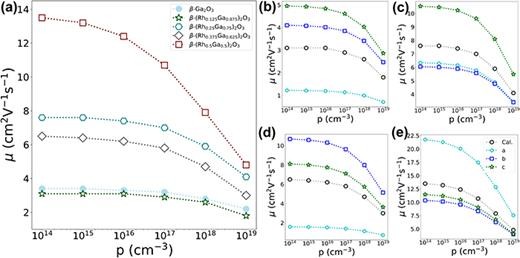
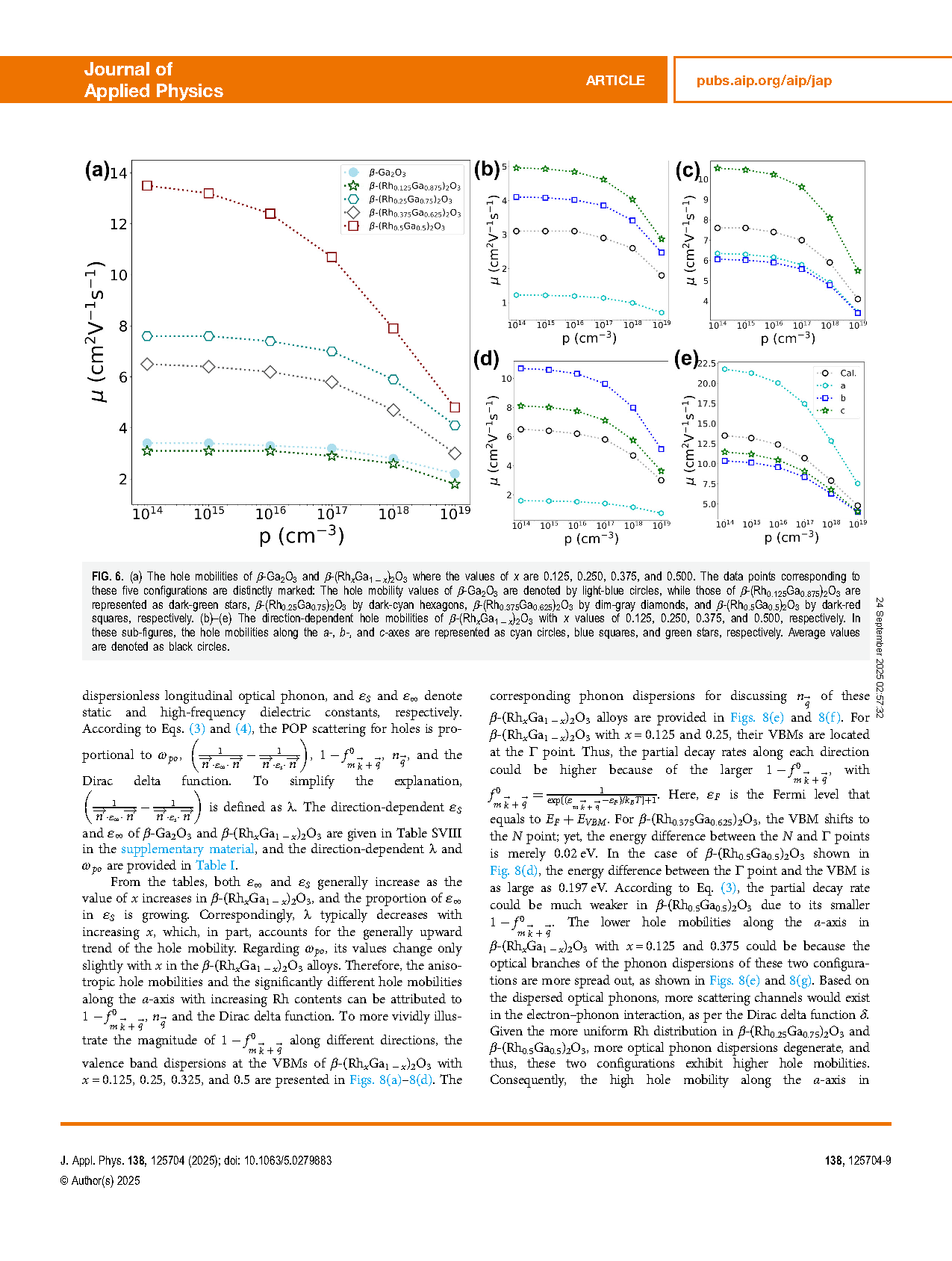
FIG. 6. (a) The hole mobilities of β-Ga2O3 and β-(RhxGa1 − x)2O3 where the values of x are 0.125, 0.250, 0.375, and 0.500. The data points corresponding to these five configurations are distinctly marked: The hole mobility values of β-Ga2O3 are denoted by light-blue circles, while those of β-(Rh0.125Ga0.875)2O3 are represented as dark-green stars, β-(Rh0.25Ga0.75)2O3 by dark-cyan hexagons, β-(Rh0.375Ga0.625)2O3 by dim-gray diamonds, and β-(Rh0.5Ga0.5)2O3 by dark-red squares, respectively. (b)–(e) The direction-dependent hole mobilities of β-(RhxGa1 − x)2O3 with x values of 0.125, 0.250, 0.375, and 0.500, respectively. In these sub-figures, the hole mobilities along the a-, b-, and c-axes are represented as cyan circles, blue squares, and green stars, respectively. Average values are denoted as black circles.
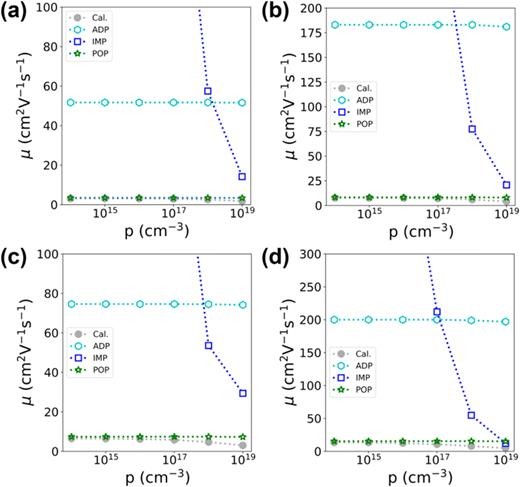
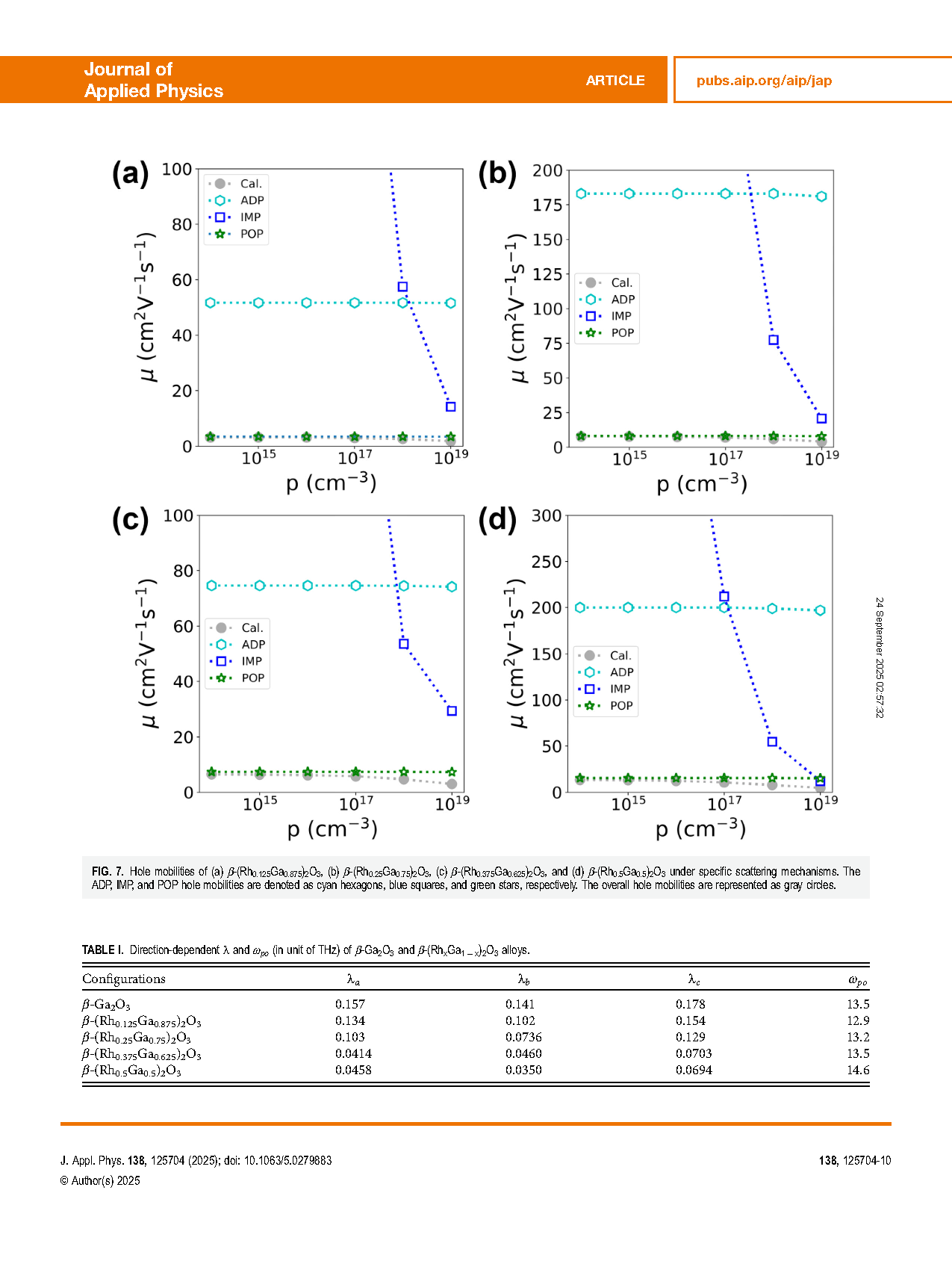
FIG. 7. Hole mobilities of (a) β-(Rh0.125Ga0.875)2O3, (b) β-(Rh0.25Ga0.75)2O3, (c) β-(Rh0.375Ga0.625)2O3, and (d) β-(Rh0.5Ga0.5)2O3 under specific scattering mechanisms. The ADP, IMP, and POP hole mobilities are denoted as cyan hexagons, blue squares, and green stars, respectively. The overall hole mobilities are represented as gray circles.
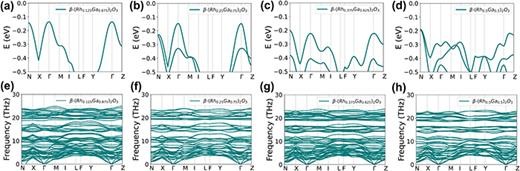
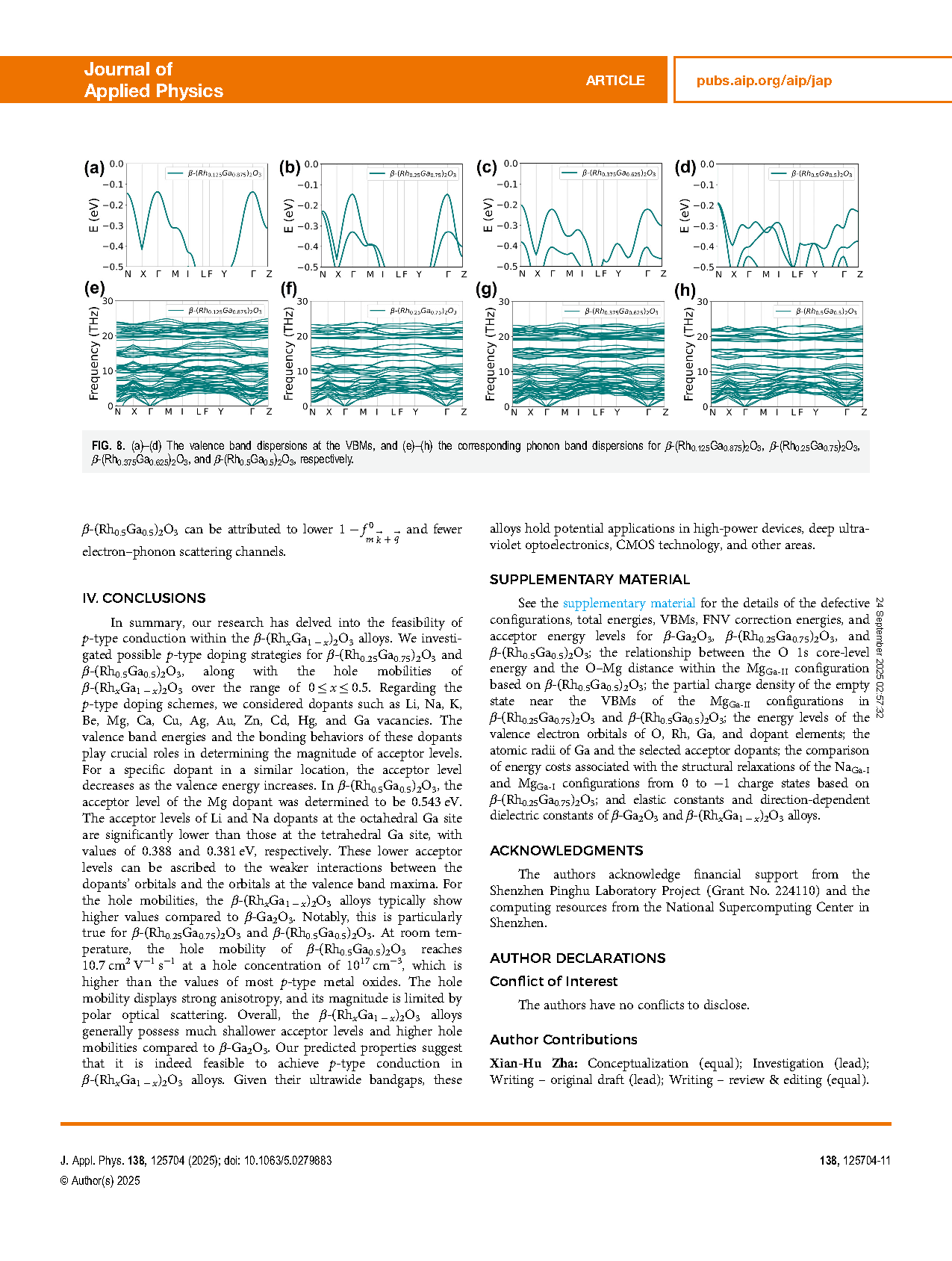
FIG. 8. (a)–(d) The valence band dispersions at the VBMs, and (e)–(h) the corresponding phonon band dispersions for β-(Rh0.125Ga0.875)2O3, β-(Rh0.25Ga0.75)2O3, β-(Rh0.375Ga0.625)2O3, and β-(Rh0.5Ga0.5)2O3, respectively.
DOI:
doi.org/10.1063/5.0279883